Note

Go to the end to download the full example code.

Uncertainty Quantification with PET-MAD

Authors:

Johannes Spies @johannes-spies

This recipe demonstrates three ways of computing errors on the outputs of ML potential-driven simulations, using as an example the PET-MAD model and its built-in uncertainty quantification (UQ) capabilities.

In particular, it demonstrates:

  1. Estimating uncertainties for single-point calculations on a full validation dataset.

  2. Computing energies in simple functions of energy predictions, namely the value of vacancy formation energies

  3. Propagating errors from energy predictions to thermodynamic averages computed over a constant-temperature MD simulation.

For more information on PET-MAD, have a look at Mazitov et al., 2025. The LLPR uncertainties are introduced in Bigi et al., 2024. For more information on dataset calibration and error propagation, see Imabalzano et al., 2021.

Optional: Adding UQ to a Model

Models compatible with metatomic can be equipped with UQ capabilities through the LLPRUncertaintyModel wrapper included with metatrain. For running this recipe, you can use a prebuilt model (the example itself downloads a model from Hugging Face). For adding UQ support to an existing model, have a look at the following scaffold. For more information on loading a dataset with the infrastructure, have a look at this section of the documentation. The pseudocode below also shows how to create an ensemble model from the last-layer parameters of a model.

from metatrain.utils.llpr import LLPRUncertaintyModel
from metatomic.torch import AtomisticModel, ModelMetadata

# You need to provide a model and datasets (wrapped in PyTorch dataloaders).
model = ...
dataloaders = {"train": ..., "val": ...}

# Wrap the model in a module capable of estimating uncertainties, estimate the
# inverse covariance on the training set, and calibrate the model on the validation
# set.
llpr_model = LLPRUncertaintyModel(model)
llpr_model.compute_covariance(dataloaders["train"])
llpr_model.compute_inverse_covariance(regularizer=1e-4)
llpr_model.calibrate(dataloaders["val"])

# In the next step, we show how to enable ensembles in PET-MAD. For that, it is
# necessary to extract the last-layer parameters of the model. The ensemble
# generation expects the parameters in a flat-vector format.
last_layer_parameters = ...

# Generate an ensemble with 128 members to compare ensemble uncertainties to LLPR
# scores.
llpr_model.generate_ensemble({"energy": last_layer_parameters}, 128)

# Save the model to disk using metatomic.
exported_model = AtomisticModel(
    llpr_model.eval(),
    ModelMetadata(),
    llpr_model.capabilities,
)
exported_model.save("models/model-with-llpr.pt")

Getting Started

At the bottom of the page, you’ll find a ZIP file containing the whole example. Note that it comes with an environment.yml file specifying all dependencies required to execute the script.

import os
import subprocess
from urllib.request import urlretrieve

import upet

import ase.geometry.rdf
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import torch
from ase import Atoms
from ase.filters import FrechetCellFilter
from ase.io.cif import read_cif
from ase.optimize.bfgs import BFGS
from ipi.utils.scripting import InteractiveSimulation
from metatomic.torch import ModelOutput
from metatomic.torch.ase_calculator import MetatomicCalculator
from metatrain.utils.data import Dataset, read_systems, read_targets
from metatrain.utils.data.system_to_ase import system_to_ase

Model Loading

All examples require a PET-MAD model with ensemble and LLPR prediction. PET-MAD v1.5.0 includes built-in LLPR uncertainty quantification, so we can use it directly. Here we use the extra-small (xs) model for speed. For production calculations, the small (s) model (size="s") is far more accurate and still very fast. We use the upet package to download the model, and load it using the ASE-compatible MetatomicCalculator wrapper, which conveniently hides computing neighbor lists in the calculator.

model_path = "models/pet-mad-xs-v1.5.0.pt"
os.makedirs("models", exist_ok=True)
upet.save_upet(model="pet-mad", size="xs", version="1.5.0", output=model_path)

calculator = MetatomicCalculator(model_path, device="cpu")

Uncertainties on a Dataset

This first example shows how to use PET-MAD to estimate uncertainties on a reference dataset. We use a reduced subset (100 structures, because of limited compute power in the CI runner) of the MAD 1.5 validation set, which contains r2SCAN references matching the level of theory used to train PET-MAD v1.5.0.

We download the full validation set from Materials Cloud and extract 100 structures with a constant stride. Then, we prepare the dataset and pass it through the model. In the final step, we visualize the predicted uncertainties and compare them to a ground truth method.

if not os.path.exists("data/mad-val-100.xyz"):
    os.makedirs("data", exist_ok=True)
    mad_val_full = "data/mad-1.5-r2scan-val.xyz"
    urlretrieve(
        "https://archive.materialscloud.org/records/18tke-tt476/"
        "files/mad-1.5-r2scan-val.xyz",
        mad_val_full,
    )
    # Extract 100 structures with constant stride from the full validation set
    full_dataset = ase.io.read(mad_val_full, index=":")
    stride = max(1, len(full_dataset) // 100)
    subset = full_dataset[::stride][:100]
    ase.io.write("data/mad-val-100.xyz", subset, format="extxyz")
    os.remove(mad_val_full)

# Read the dataset's structures.
systems = read_systems("data/mad-val-100.xyz")

# Read the dataset's targets.
target_config = {
    "energy": {
        "quantity": "energy",
        "read_from": "data/mad-val-100.xyz",
        "reader": "ase",
        "key": "atomization_energy",
        "unit": "eV",
        "type": "scalar",
        "per_atom": False,
        "num_subtargets": 1,
        "forces": False,
        "stress": False,
        "virial": False,
    },
}
targets, infos = read_targets(target_config)  # type: ignore

# Wrap in a `metatrain` compatible way.
dataset = Dataset.from_dict({"system": systems, **targets})

After preparation, the dataset can be passed through the model using the calculator to obtain energy predictions and LLPR scores.

# Convert the systems to an ASE-native `Atoms` object
systems = [system_to_ase(sample["system"]) for sample in dataset]
outputs = {
    # Request the uncertainty in the atomic energy predictions
    "energy": ModelOutput(),  # (Needed to request the uncertainties)
    "energy_uncertainty": ModelOutput(),
}
results = calculator.run_model(systems, outputs)

# Extract the requested results
predicted_energies = results["energy"][0].values.squeeze()
predicted_uncertainties = results["energy_uncertainty"][0].values.squeeze()

Compute the true prediction error by comparing the predicted energy to the reference value from dataset.

# Reference values from dataset.
ground_truth_energies = torch.stack(
    [sample["energy"][0].values.squeeze() for sample in dataset]
)

# Compute squared distance between predicted energy and reference value.
empirical_errors = torch.abs(predicted_energies - ground_truth_energies)

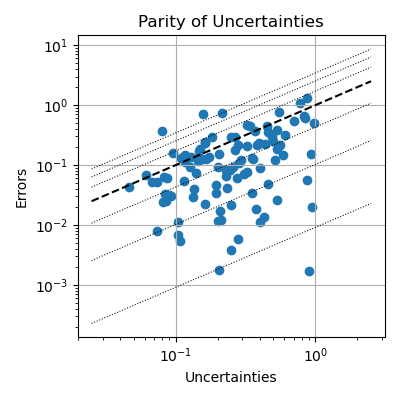
After gathering predicted uncertainties and computing ground truth error metrics, we can compare them to each other. Similar to figure S4 of the PET-MAD paper, we present the data in using a parity plot. For more information about interpreting this type of plot, see Appendix F.7 of Bigi et al., 2024. Note that both the x- and the y-axis use a logarithmic scale, which is more suitable for inspecting uncertainty values. Because we are using a heavily reduced dataset (only 100 structures) from the MAD validation set, the parity plot looks very sparse.

# Hard-code the zoomed in region of the plot and iso-lines.
quantile_lines = [0.00916, 0.10256, 0.4309805, 1.71796, 2.5348, 3.44388]
min_val, max_val = 2.5e-2, 2.5

# Create the parity plot.
plt.figure(figsize=(4, 4))
plt.grid()
plt.gca().set(
    title="Parity of Uncertainties",
    ylabel="Errors",
    xlabel="Uncertainties",
)
plt.loglog()

# Plot iso lines.
plt.plot([min_val, max_val], [min_val, max_val], ls="--", c="k")
for factor in quantile_lines:
    plt.plot([min_val, max_val], [factor * min_val, factor * max_val], "k:", lw=0.75)

# Add actual samples.
plt.scatter(predicted_uncertainties, empirical_errors)

plt.tight_layout()
Parity of Uncertainties

Uncertainties in Vacancy Formation Energies

One can use ensemble uncertainty quantification to estimate the error in predicting vacancy formation energies, which we show in this example.

In this part, we use an aluminum crystal as an example system. The structure file can be downloaded from Material Project as a .cif file. We’ve included such a file with the recipe.

The following code loads the structure, computes the energy before creating a defect, creates a defect, runs a structural optimization, and computes the energy after the optimization. The energy difference can be used to estimate the vacancy formation energy.

# Load the crystal from the Materials Project and create a supercell (not strictly
# necessary).
crystal_structure = "data/Al_mp-134_conventional_standard.cif"
atoms: Atoms = read_cif(crystal_structure)  # type: ignore
supercell = atoms * 2
supercell.calc = calculator
N = len(supercell)  # store the number of atoms

We now compute the vacancy formation energy by keeping track of the ensemble energies at different stages. Note that calling .get_potential_energy() on an Atoms object triggers computing the ensemble values.

# Get ensemble energy before creating the vacancy
outputs = ["energy", "energy_uncertainty", "energy_ensemble"]
outputs = {o: ModelOutput() for o in outputs}
results = calculator.run_model(supercell, outputs)
bulk = results["energy_ensemble"][0].values

# Remove an atom (last atom in this case) to create a vacancy
i = -1
supercell.pop(i)

# Get ensemble energy right after creating the vacancy
results = calculator.run_model(supercell, outputs)
right_after_vacancy = results["energy_ensemble"][0].values

# Run structural optimization optimizing both positions and cell layout.
ecf = FrechetCellFilter(supercell)
bfgs = BFGS(ecf)  # type: ignore
bfgs.run()

# get ensembele energy after optimization
results = calculator.run_model(supercell, outputs)
vacancy = results["energy_ensemble"][0].values

      Step     Time          Energy          fmax
BFGS:    0 14:27:19     -127.227844        0.252987
BFGS:    1 14:27:19     -127.231949        0.255207
BFGS:    2 14:27:19     -127.262093        0.267222
BFGS:    3 14:27:19     -127.270676        0.266933
BFGS:    4 14:27:19     -127.349586        0.293387
BFGS:    5 14:27:19     -127.383453        0.243963
BFGS:    6 14:27:20     -127.422028        0.058580
BFGS:    7 14:27:20     -127.422516        0.043295

Compute vacancy formation energy for each ensemble member.

vacancy_formation = vacancy - (N - 1) / N * bulk

Put all ensemble energies in a dataframe and compute the desired statistics.

# This dataframe contains each stage's energies in a single column.
named_stages = [
    ("Before creating vacancy", bulk),
    ("Right after creating vacancy", right_after_vacancy),
    ("Energy of optimized vacancy", vacancy),
    ("Vacancy formation energy", vacancy_formation),
]
df = pd.DataFrame.from_dict(
    {
        # Convert the PyTorch tensors to flat NumPy vectors
        k: v.detach().numpy().squeeze()
        for k, v in named_stages
    }
)

# Compute statistics (mean, variance, and standard deviation) on the ensemble energies.
df = pd.DataFrame(dict(mean=df.mean(), var=df.var(), std=df.std()))
df
mean var std
Before creating vacancy -131.802216 1.531852 1.237680
Right after creating vacancy -127.227837 1.401798 1.183975
Energy of optimized vacancy -127.422516 1.564886 1.250954
Vacancy formation energy 0.260880 0.009630 0.098133


Uncertainty Propagation with MD

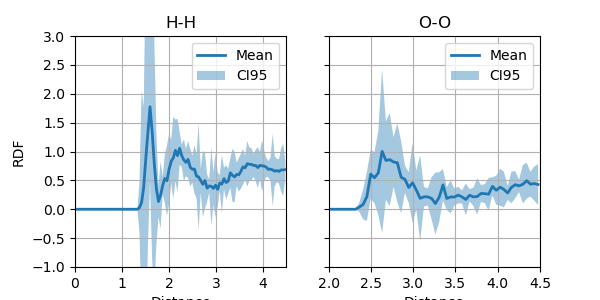
This example shows how to use i-PI to propagate error estimates from an ensemble to output observables. In this example, we use a box with period boundary conditions housing 32 water molecules. As an observable, we inspect the Radial Distribution Function (RDF) between hydrogen-hydrogen and oxygen-oxygen bonds.

First, we run a simulation with i-PI generating a trajectory and logging other metrics. The trajectory and committee energies can be used in a subsequent postprocessing step to obtain RDFs using ASE. These can be re-weighted to propagate errors from the committee uncertainties to the observed RDFs.

Note also that we set a uncertainty_threshold option in the driver. When running from the command line, this will output a warning every time one of the atomic energy is estimated to have an uncertainty above that threshold (in eV/atom).

# Load configuration and run simulation.
with open("data/h2o-32.xml") as f:
    xml_input = f.read()

# prints the relevant sections of the input file
print(xml_input[:883][-334:])

sim = InteractiveSimulation(xml_input)

rue">
    <pes>metatomic</pes>
    <parameters>
        { template:data/h2o-32.xyz,model:models/pet-mad-xs-v1.5.0.pt,device:cpu,
          non_conservative:False,energy_ensemble:True,
          check_consistency:False,
          uncertainty_threshold:7.0e-2
        }
    </parameters>
  </ffdirect>
  <system>
    <initialize nbeads=
 @system: Initializing system object
 @simulation: Initializing simulation object
@ RANDOM SEED: The seed used in this calculation was 23658
 @init_file: Initializing from file data/h2o-32.xyz. Dimension: length, units: angstrom, cell_units: automatic
 @init_file: Initializing from file data/h2o-32.xyz. Dimension: length, units: automatic, cell_units: automatic
 @init_file: Initializing from file data/h2o-32.xyz. Dimension: length, units: automatic, cell_units: automatic
 @init_file: Initializing from file data/h2o-32.xyz. Dimension: length, units: automatic, cell_units: automatic
 @init_file: Initializing from file data/h2o-32.xyz. Dimension: length, units: automatic, cell_units: automatic
 @initializer: Resampling velocities at temperature 300.0 kelvin
 --- begin input file content ---

  <simulation verbosity='medium'>
    <output prefix='h2o-32'>
      <properties filename='out' stride='10'>[ time{picosecond}, temperature{kelvin}, kinetic_md ]</properties>
      <trajectory filename='pos' format='ase' stride='10'>positions</trajectory>
      <trajectory filename='committee_pot' stride='10' extra_type='committee_pot'>extras</trajectory>
      <trajectory filename='atomic_error' stride='10' extra_type='energy_uncertainty'>extras</trajectory>
    </output>
    <prng>
      <seed>23658</seed>
    </prng>
    <ffdirect name='nocons' pbc='true'>
      <pes>metatomic</pes>
      <parameters>{ template:data/h2o-32.xyz,model:models/pet-mad-xs-v1.5.0.pt,device:cpu,
          non_conservative:False,energy_ensemble:True,
          check_consistency:False,
          uncertainty_threshold:7.0e-2
        }</parameters>
    </ffdirect>
    <system>
      <initialize nbeads='1'>
        <file mode='xyz' units='angstrom'>data/h2o-32.xyz</file>
        <velocities mode='thermal' units='kelvin'>300</velocities>
      </initialize>
      <forces>
        <force forcefield='nocons'>
        </force>
      </forces>
      <ensemble>
        <temperature units='kelvin'>300</temperature>
      </ensemble>
      <motion mode='dynamics'>
        <fixcom>True</fixcom>
        <dynamics mode='nvt'>
          <timestep units='femtosecond'>0.5</timestep>
          <thermostat mode='langevin'>
            <tau units='femtosecond'>50</tau>
          </thermostat>
        </dynamics>
      </motion>
    </system>
  </simulation>
 ---  end input file content  ---
 @system.bind: Binding the forces

Run the simulation.

# NB: To get better estimates, set this to a higher number (perhaps 10000) to
# run the simulation for a longer time.
sim.run(400)

!W! the estimated atomic energy uncertainty 3.3381 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3350 eV/atom exceeds the selected threshold of 0.0700 eV/atom
@simulation.run: Average timings at MD step       0. t/step: 8.37811e-01
!W! the estimated atomic energy uncertainty 3.3276 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3181 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3092 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3029 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.2997 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.2988 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.2989 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.2996 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3001 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3005 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3004 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3010 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3029 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3067 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3127 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3200 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3265 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3313 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3336 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3324 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3289 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3247 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3214 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3199 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3206 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3232 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3269 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3307 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3341 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3367 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3388 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3409 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3436 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3465 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3501 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3538 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3573 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3593 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3598 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3582 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3553 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3516 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3479 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3452 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3437 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3427 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3419 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3410 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3395 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3381 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3372 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3368 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3373 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3388 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3408 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3424 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3439 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3451 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3466 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3484 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3498 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3506 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3509 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3511 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3510 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3507 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3505 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3505 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3513 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3526 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3544 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3564 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3586 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3611 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3635 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3661 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3683 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3696 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3697 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3694 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3687 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3681 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3673 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3659 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3649 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3634 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3618 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3599 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3577 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3553 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3525 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3498 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3475 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3460 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3455 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3456 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3466 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3481 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3492 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3501 eV/atom exceeds the selected threshold of 0.0700 eV/atom
@simulation.run: Average timings at MD step     100. t/step: 9.43089e-02
!W! the estimated atomic energy uncertainty 3.3504 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3511 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3524 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3544 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3572 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3600 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3633 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3669 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3703 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3736 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3758 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3770 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3773 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3768 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3760 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3748 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3733 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3713 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3691 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3667 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3644 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3622 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3604 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3589 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3575 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3563 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3551 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3540 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3526 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3513 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3503 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3492 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3476 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3456 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3439 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3418 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3400 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3389 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3382 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3384 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3390 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3406 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3433 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3466 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3501 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3529 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3553 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3575 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3599 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3626 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3653 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3676 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3687 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3687 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3681 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3670 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3658 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3650 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3647 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3642 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3634 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3626 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3617 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3603 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3583 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3560 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3527 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3499 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3479 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3458 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3430 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3397 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3362 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3329 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3302 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3288 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3284 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3291 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3309 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3335 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3363 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3392 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3418 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3444 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3470 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3493 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3512 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3528 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3539 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3543 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3548 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3549 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3549 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3551 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3556 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3566 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3572 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3572 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3565 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3554 eV/atom exceeds the selected threshold of 0.0700 eV/atom
@simulation.run: Average timings at MD step     200. t/step: 8.92665e-02
!W! the estimated atomic energy uncertainty 3.3539 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3525 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3508 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3493 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3481 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3470 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3462 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3461 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3466 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3471 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3472 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3470 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3469 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3467 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3466 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3466 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3464 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3460 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3455 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3453 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3456 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3462 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3474 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3487 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3505 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3527 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3558 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3597 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3642 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3692 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3739 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3780 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3810 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3820 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3818 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3800 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3767 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3726 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3678 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3632 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3595 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3569 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3550 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3536 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3526 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3527 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3532 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3541 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3561 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3585 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3613 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3636 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3652 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3659 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3649 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3627 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3593 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3555 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3525 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3502 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3492 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3489 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3497 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3507 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3523 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3540 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3561 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3583 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3608 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3636 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3664 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3685 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3695 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3690 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3674 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3655 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3631 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3606 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3588 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3577 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3575 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3580 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3588 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3593 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3598 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3602 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3601 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3601 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3605 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3615 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3629 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3636 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3631 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3620 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3606 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3592 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3579 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3569 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3562 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3556 eV/atom exceeds the selected threshold of 0.0700 eV/atom
@simulation.run: Average timings at MD step     300. t/step: 9.15641e-02
!W! the estimated atomic energy uncertainty 3.3553 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3554 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3556 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3561 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3573 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3588 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3606 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3622 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3636 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3650 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3668 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3688 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3708 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3727 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3738 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3742 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3739 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3725 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3708 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3692 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3679 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3668 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3664 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3664 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3663 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3658 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3654 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3654 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3660 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3665 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3666 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3661 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3652 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3630 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3601 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3568 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3533 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3507 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3488 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3473 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3463 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3455 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3447 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3446 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3448 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3456 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3470 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3488 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3507 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3518 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3514 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3502 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3483 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3470 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3465 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3459 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3450 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3441 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3428 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3422 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3419 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3416 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3412 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3407 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3408 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3416 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3431 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3450 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3472 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3486 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3496 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3505 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3520 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3535 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3551 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3568 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3585 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3600 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3613 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3624 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3634 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3640 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3641 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3640 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3638 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3637 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3636 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3635 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3633 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3635 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3638 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3638 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3635 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3628 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3620 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3613 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3607 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3602 eV/atom exceeds the selected threshold of 0.0700 eV/atom
!W! the estimated atomic energy uncertainty 3.3603 eV/atom exceeds the selected threshold of 0.0700 eV/atom

Load the trajectories and compute the per-frame RDFs Note that ASE applies a weird normalization to the partial RDFs, which require a correction to recover the usual asymptotic behavior at large distances.

frames: list[Atoms] = ase.io.read("h2o-32.pos_0.extxyz", ":")  # type: ignore

# Our simulation should only include water molecules. (types: hydrogen=1, oxygen=8)
assert set(frames[0].numbers.tolist()) == set([1, 8])

# Compute the RDF of each frame (for H-H and for O-O)
num_bins = 250
rdfs_hh = []
rdfs_oo = []
xs = None
for atoms in frames:
    # Compute H-H distances
    bins, xs = ase.geometry.rdf.get_rdf(  # type: ignore
        atoms, 4.5, num_bins, elements=[1, 1]
    )

    # smoothen the RDF a bit (not enough data...)
    bins[2:-2] = (
        bins[:-4] * 0.1
        + bins[1:-3] * 0.2
        + bins[2:-2] * 0.4
        + bins[3:-1] * 0.2
        + bins[4:] * 0.1
    )
    rdfs_hh.append(bins)

    # Compute O-O distances
    bins, xs = ase.geometry.rdf.get_rdf(  # type: ignore
        atoms, 4.5, num_bins, elements=[8, 8]
    )
    bins[2:-2] = (
        bins[:-4] * 0.1
        + bins[1:-3] * 0.2
        + bins[2:-2] * 0.4
        + bins[3:-1] * 0.2
        + bins[4:] * 0.1
    )
    rdfs_oo.append(bins)

rdfs_hh = np.stack(rdfs_hh, axis=0)
rdfs_oo = np.stack(rdfs_oo, axis=0)

Run the i-PI re-weighting utility as a post-processing step.

# Save RDFs such that they can be read from i-PI.
np.savetxt("h2o-32_rdfs_h-h.txt", rdfs_hh)
np.savetxt("h2o-32_rdfs_o-o.txt", rdfs_oo)

# Run the re-weighting tool from i-PI for H-H and O-O
for ty in ["h-h", "o-o"]:
    infile = f"h2o-32_rdfs_{ty}.txt"
    outfile = f"h2o-32_rdfs_{ty}_reweighted.txt"
    cmd = (
        f"i-pi-committee-reweight h2o-32.committee_pot_0 {infile} --input"
        " data/h2o-32.xml"
    )
    print("Executing command:", "\t" + cmd, sep="\n")
    cmd = cmd.split()
    with open(outfile, "w") as out:
        process = subprocess.run(cmd, stdout=out)

Executing command:
        i-pi-committee-reweight h2o-32.committee_pot_0 h2o-32_rdfs_h-h.txt --input data/h2o-32.xml
Executing command:
        i-pi-committee-reweight h2o-32.committee_pot_0 h2o-32_rdfs_o-o.txt --input data/h2o-32.xml

Load and display the RDFs after re-weighting. Note that the results might not noisy due to the small number of MD steps.

# Load the reweighted RDFs.
rdfs_hh_reweighted = np.loadtxt("h2o-32_rdfs_h-h_reweighted.txt")
rdfs_oo_reweighted = np.loadtxt("h2o-32_rdfs_o-o_reweighted.txt")

# Extract columns.
rdfs_hh_reweighted_mu = rdfs_hh_reweighted[:, 0]
rdfs_hh_reweighted_err = rdfs_hh_reweighted[:, 1]
rdfs_hh_reweighted_committees = rdfs_hh_reweighted[:, 2:]

rdfs_oo_reweighted_mu = rdfs_oo_reweighted[:, 0]
rdfs_oo_reweighted_err = rdfs_oo_reweighted[:, 1]
rdfs_oo_reweighted_committees = rdfs_oo_reweighted[:, 2:]

# Display results.
fig, axs = plt.subplots(figsize=(6, 3), sharey=True, ncols=2, constrained_layout=True)
for title, ax, mus, std, xlim in [
    ("H-H", axs[0], rdfs_hh_reweighted_mu, rdfs_hh_reweighted_err, (1.0, 4.5)),
    ("O-O", axs[1], rdfs_oo_reweighted_mu, rdfs_oo_reweighted_err, (2.0, 4.5)),
]:
    ylabel = "RDF" if title == "H-H" else None
    ax.set(title=title, xlabel="Distance", ylabel=ylabel, xlim=xlim, ylim=(-0.1, 3.7))
    ax.grid()
    ax.plot(xs, mus, label="Mean", lw=0.5)
    z95 = 1.96
    rdfs_ci95 = (mus - z95 * std, mus + z95 * std)
    ax.fill_between(xs, *rdfs_ci95, alpha=0.5, label="CI95")
    ax.legend()
H-H, O-O

Total running time of the script: (1 minutes 0.495 seconds)

Gallery generated by Sphinx-Gallery